Mathe für Anfänger (11)
1. Aug.. 2009 · 4.909 mal gelesen | 5 Kommentare »
Und auch heute wieder ein weiterer Teil aus der Reihe “Mathe für Anfänger“.
Heute: “Addition positiver und negativer Zahlen”.
Ist das Ergebnis der Addition einer positiven Zahl mit einer anderen Zahl kleiner als die erste Zahl, so muss der zweite Summand negativ gewesen sein.
Kurz: ist A + B < A folgt daraus zwangsläufig B < 0
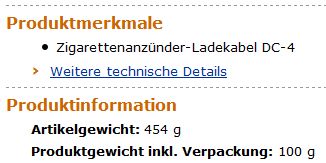 Bei Amazon.de gibt es anscheinend inzwischen auch die Möglichkeit, Kleinteile per Helium-Ballon zu verschicken.
Bei Amazon.de gibt es anscheinend inzwischen auch die Möglichkeit, Kleinteile per Helium-Ballon zu verschicken.
Oder wie könnte man sonst erklären, dass ein Artikel alleine 454 g wiegt, mit Verpackung aber nur noch 100 g ?
Mathe für Anfänger (10)
19. Juli. 2009 · 5.006 mal gelesen | 6 Kommentare »
Mathe ist ganz einfach – vor allem Prozentrechnung:
Wenn auf einer Flasche Ariel steht: ‚+10% mehr Inhalt‘, dann heißt das, dass man erst mal den Grundwert um 10% gesenkt hat, um ihn dann wieder um 11,1% zu erhöhen, wobei dann wieder der ursprüngliche Grundwert heraus kommt. Auf der Flasche steht dann aber nicht ‚11,1% mehr‘, sondern nur ’10 % mehr‘, sicher mit der Begründung, dass ja eh beides nicht stimmt, weil der Inhalt statt 1,5 L nur noch 1,4 L beträgt, was wiederum einer Verringerung um 6,67 % entspricht.
Man sieht: Mathe ist ganz einfach – vor allem Prozentrechnung.
Zum besseren Verständnis und zur Wiederholung dieser Lektion, das Ganze noch einmal mit einem praktischen Beispiel in Bildern:
[gefunden bei Duerrbi.de, via]
Mathe für Anfänger (9)
8. Juni. 2009 · 3.407 mal gelesen | 2 Kommentare »
Der Tag nach irgendwelchen Wahlen ist immer prädestiniert für einen weiteren Teil aus der Reihe “Mathe für Anfänger“.
Heute: “Prozentrechnung – Grundwert/Prozentwert”.
2009 ist ein sogenanntes ‚Superwahljahr‘. Ich würde es als ‚Superschreikrampfjahr‘ für all jene bezeichnen, die ihren Lebensunterhalt damit verdienen, anderen die Prozentrechnung richtig beizubringen.
Nach jedem Wahlsonntag haben die Politikerreden mit Schreikrampfpotential Hochkonjunktur. Zur Verdeutlichung ein zufällig ausgewähltes Beispiel unter vielen:
CDU-Generalsekretär Ronald Pofalla sprach am Abend von einem Vertrauensbeweis für die Union […]. Die Union habe gegenüber der Bundestagswahl 2005 zugelegt, rechnete er vor.
Profalla rechnet vor – Pumi rechnet nach:
Bundestagswahl 2005:
CDU/CSU 35,2% der abgegebenen Stimmen, Wahlbeteiligung 77,7%
Europaparlamentswahl 2009:
CDU/CSU 37,9% der abgegebenen Stimmen, Wahlbeteiligung 42,5%
Wenn man diese Zahlen überhaupt vergleichen will/kann, dann nur auf der Ebene von „Wie viele der Wahlberechtigten haben CDU/CSU gewählt?“
Dazu multipliziert man die zugehörigen Prozentfaktoren (35,2% = 35,2/100 = 0,352) miteinander:
2005: 35,2% von 77,7% = 0,352 * 0,777 = 0,2735= 27,4%
2009: 37,9% von 42,5% = 0,379 * 0,425 = 0,161= 16,1%
Haben also 2005 noch 27,4% der Wahlberechtigten CDU/CSU gewählt, waren es 2009 gerade einmal 16,1%.
Schlussbemerkung: solche Apfel-Birnen-Vergleiche hört man natürlich nicht nur bei Herrn Profalla. Nein, sie sind (wo es gerade passt) allgegenwärtig bei Politikern aller Richtungen und in allen Medien.
Nachtrag: Falls irgendwer in diesem Beitrag eine politische Botschaft sucht – beabsichtigt war allerhöchstens diese:
Ich finde es erschreckend, in einer Demokratie zu leben, in der fast 3 von 5 Menschen ihr Recht zu wählen so scheißegal ist, dass sie nicht Wählen gehen.
Mathe für Anfänger (8)
27. Mai. 2009 · 3.360 mal gelesen | 3 Kommentare »
Und auch heute wieder ein weiterer Teil aus der Reihe “Mathe für Anfänger“.
Heute: “Multiplikation mit Zehnerpotenzen”.
- Möchte man eine ganze Zahl mit 10 multiplizieren, so fügt man einfach eine Null an. ‚Zehnmal mal so viel wie‘ oder ‚das Zehnfache von‘ 4400 ist also 44000.
- Soll die Zahl mit 100 multipliziert werden, fügt man zwei Nullen an. 440000 ist also ‚hundert mal mehr‘ als 4400.
- Werden drei Nullen angefügt, so entspricht dies dem Faktor 1000. 100000000 ist also das Tausendfache von 100000.
- Sind mehr als drei Nullen im Spiel, befindet man sich wohl in der Redaktion von Stern.de, wo man am Samstag diesen Artikel veröffentlicht hat:

Anscheinend hat man aber über das Wochenende Nachhilfe bekommen und bemerkt, dass bei so vielen Nullen doch etwas schief gelaufen sein könnte. Der Artikel hat jetzt einen Fehler weniger und sieht so aus:

Man hat sich bemüht…
[via]
Nachtrag: bei Spiegel Online hat man auch Probleme mit Nullen oder falschen Stellen:
„Der erste Transfer aus der Bundesliga, für den eine zweistellige Summe überwiesen wurde, war der von Jörg Heinrich, der 1998 für 12,5 Millionen Euro vom BVB nach Florenz transferiert wurde.“
Mathe für Anfänger (7)
23. Feb.. 2009 · 4.573 mal gelesen | 1 Kommentar »
Und auch heute wieder ein weiterer Teil aus der Reihe “Mathe für Anfänger“.
Heute: „Proportionale Zuordnungen“.
Eine Zuordnung nennt man dann proportional, wenn dem n-fachen der einen Größe auch das n-fache der zweiten Größe zugeordnet wird.
So ist z.B. die Zuordnung ‚Zeit -> Weg‘ bei konstanter Geschwindigkeit proportional. Auch die Zuordnung ‚Schneevolumen -> Gewicht‘ ist bei gleich bleibender Schneekonsistenz proportional.
Weitere Beispiele:
- ‚geräumte Fläche -> Volumen der Schneehaufen‘
- ‚Schneeschipp-Dauer -> Anzahl der gehörten blöden Kommentare‘
- ‚Anzahl der entfernten Dachlawinen -> Stärke der Rückenschmerzen‘
Einfach zu erkennen sind proportionale Zuordnungen, wenn man sie mit ‚je mehr…, desto mehr…‘ beschreiben kann.
Also: Je mehr Schnee man räumen muss, desto mehr freut man sich auf den Frühling.
Mathe für Anfänger (6)
3. Jan.. 2009 · 2.563 mal gelesen | Kommentar schreiben »
Auch wenn gerade Ferien sind, hier ein weiterer Teil aus der Reihe “Mathe für Anfänger“.
Diesmal: Rechnen mit Bruch-Verhältnissen (Grundstufe – unterstes Niveau).
Der Wert eines Bruches nimmt bei zunehmendem Nenner und gleichem Zähler ab.
Wie gesagt: unterstes Niveau. Jedes Kind weiß, wenn ich meine Süßigkeiten mit fünf Leuten teilen muss bekomme ich weniger, als wenn ich sie mit drei Leuten teilen muss.
Jedes Kind weiß es – aber nicht die Fachleute Zuständigen für Straßenverkehr bei Bild.de :

(gefunden bei bildblog.de)
Mathe für Anfänger (5)
28. Dez.. 2008 · 2.664 mal gelesen | Kommentar schreiben »
Auf eine Anfrage einer interessierten Leserin hin, hier ein weiterer Teil aus der Reihe „Mathe für Anfänger„:
Die Frage:
„Ich bin grade am Putzen, und finde es doch immer wieder beeindruckend, wie viel Dreck auf so wenig Platz passt. Gibt es dazu eigentlich eine mathematische Formel??“
Meine Antwort:
Für dein Dreck-Problem habe ich noch keine mathematische Formel gefunden. Ich habe mich dem Problem aber experimentell genähert. Erste Vermutungen am praktischen Beispiel meines Schlafzimmers gehen in diese Richtung:
Sei d(t) die Gesamtmenge des Drecks auf einer begrenzten Fläche nach einer staubsaugerfreien Zeitdauer t, so ist der Grenzwert von d(t) für t gegen Unendlich auch unendlich groß, d.h. d(t) ist vermutlich divergent.
Mathe für Anfänger (4)
17. Dez.. 2008 · 3.939 mal gelesen | Kommentar schreiben »
Endlich mal wieder gibt es ein neues Kapitel der Reihe „Mathe für Anfänger„.
Heute: „Achsensymmetrie“.
Das Schaubild K einer Funktion f(x) ist symmetrisch zu der Geraden x = x0 wenn für alle h gilt:
f(x0+h) = f(x0-h)
Deutlich einfacher wird dieser Sachverhalt den Mathe-Schülern schon vor der Pupertät gelehrt:
Eine Figur ist symmetrisch, wenn es zu jedem Punkt P einen Abbildpunkt P‘ gibt, der den gleichen Abstand wie P zu jedem Punkt auf der Symmetrieachse hat.
Oder noch einfacher: auf beiden Seiten der Spiegelachse ist das gleiche – nur spiegelverkehrt.
Warum diese Mathe-Lektion?
Nun ja: als Hobby-Fotograf interessiere ich mich natürlich für die Werke der Profis. Und so habe ich bei National Geographic den ‚Photo Contest‚ gefunden. Genauer – ich habe einen der ‚2008 winners‘ gefunden:

Gute Bildbearbeitungs-Programme sind nicht alles. Man sollte trotzdem noch nachdenken.
Fazit: Leute passt in Mathe besser auf – dann merkt man es nicht so schnell, wenn ihr bei Fotowettbewerben bescheißen wollt!
Mathe für Anfänger (3)
23. Nov.. 2008 · 5.528 mal gelesen | Kommentar schreiben »
Es wird mal wieder Zeit für eine neue Lektion Mathe für Anfänger. Heute: „Einfache Subtraktionsrechnung“.
Bei einem der größten Radsport-Informationsdienste (ja richtig: derselbe, der schon hier einen großen Auftritt hatte) findet sich diese Nachricht:
Erstmals seit 12 Jahren wieder in den Niederlanden
Tour de France 2010 startet in Rotterdam
Wer keine Numerophobie hat, darf beim Ratespiel mitmachen. Wann war die Tour wohl zuletzt in den Niederlanden? Wer nicht selbst rechnen möchte, liest in dem Artikel weiter:
Erstmals seit 12 Jahren startet die Tour damit wieder in den Niederlanden. Im Jahr 1996 fand der Auftakt in ’s-Hertogenbosch statt.
Hier wäre wohl dringend ein bisschen Nachhilfe in Mathe hilfreich.
2010 – 1996 = 14
Mathe für Anfänger (2)
24. Mai. 2008 · 4.547 mal gelesen | 3 Kommentare »
Es wird mal wieder Zeit für eine neue Lektion „Mathe für Anfänger“ – Heute „Prozentrechnen“:

Der Prozentsatz lässt sich berechnen, indem man den Prozentwert (in diesem Fall die Anzahl der positiven Bewertungen) durch den Grundwert (in diesem Fall die Anzahl aller Bewertungen) dividiert und das Ergebnis mit 100 multipliziert.
Allgemein dürfte dies ein Resultat mit maximal einem Komma ergeben – selbst wenn der Grundwert 15 Millionen übersteigt…
